Guide to the Sequential Model

Defining a Model

The sequential model is a linear stack of layers.

You create a sequential model by calling the keras_model_sequential() function then a series of layer functions:

library(keras)

model <- keras_model_sequential() 
model %>% 
  layer_dense(units = 32, input_shape = c(784)) %>% 
  layer_activation('relu') %>% 
  layer_dense(units = 10) %>% 
  layer_activation('softmax')

Note that Keras objects are modified in place which is why it’s not necessary for model to be assigned back to after the layers are added.

Print a summary of the model’s structure using the summary() function:

summary(model)

Model
________________________________________________________________________________
Layer (type)                        Output Shape                    Param #     
================================================================================
dense_1 (Dense)                     (None, 256)                     200960      
________________________________________________________________________________
dropout_1 (Dropout)                 (None, 256)                     0           
________________________________________________________________________________
dense_2 (Dense)                     (None, 128)                     32896       
________________________________________________________________________________
dropout_2 (Dropout)                 (None, 128)                     0           
________________________________________________________________________________
dense_3 (Dense)                     (None, 10)                      1290        
================================================================================
Total params: 235,146
Trainable params: 235,146
Non-trainable params: 0
________________________________________________________________________________

Input Shapes

The model needs to know what input shape it should expect. For this reason, the first layer in a sequential model (and only the first, because following layers can do automatic shape inference) needs to receive information about its input shape.

As illustrated in the example above, this is done by passing an input_shape argument to the first layer. This is a list of integers or NULL entries, where NULL indicates that any positive integer may be expected. In input_shape, the batch dimension is not included.

If you ever need to specify a fixed batch size for your inputs (this is useful for stateful recurrent networks), you can pass a batch_size argument to a layer. If you pass both batch_size=32 and input_shape=c(6, 8) to a layer, it will then expect every batch of inputs to have the batch shape (32, 6, 8).

Compilation

Before training a model, you need to configure the learning process, which is done via the compile() function. It receives three arguments:

An optimizer. This could be the string identifier of an existing optimizer (e.g. as “rmsprop” or “adagrad”) or a call to an optimizer function (e.g. optimizer_sgd()).
A loss function. This is the objective that the model will try to minimize. It can be the string identifier of an existing loss function (e.g. “categorical_crossentropy” or “mse”) or a call to a loss function (e.g. loss_mean_squared_error()).
A list of metrics. For any classification problem you will want to set this to metrics = c('accuracy'). A metric could be the string identifier of an existing metric or a call to metric function (e.g. metric_binary_crossentropy()).

Here’s the definition of a model along with the compilation step (the compile() function has arguments appropriate for a multi-class classification problem):

# For a multi-class classification problem
model <- keras_model_sequential() 
model %>% 
  layer_dense(units = 32, input_shape = c(784)) %>% 
  layer_activation('relu') %>% 
  layer_dense(units = 10) %>% 
  layer_activation('softmax')

model %>% compile(
  optimizer = 'rmsprop',
  loss = 'categorical_crossentropy',
  metrics = c('accuracy')
)

Here’s what compilation might look like for a mean squared error regression problem:

model %>% compile(
  optimizer = optimizer_rmsprop(lr = 0.002),
  loss = 'mse'
)

Here’s compilation for a binary classification problem:

model %>% compile( 
  optimizer = optimizer_rmsprop(),
  loss = loss_binary_crossentropy,
  metrics = metric_binary_accuracy
)

Here’s compilation with a custom metric:

# create metric using backend tensor functions
metric_mean_pred <- function(y_true, y_pred) {
  k_mean(y_pred) 
}

model %>% compile( 
  optimizer = optimizer_rmsprop(),
  loss = loss_binary_crossentropy,
  metrics = c('accuracy', 
              'mean_pred' = metric_mean_pred)
)

Training

Keras models are trained on R matrices or higher dimensional arrays of input data and labels. For training a model, you will typically use the fit() function.

Here’s a single-input model with 2 classes (binary classification):

# create model
model <- keras_model_sequential()

# add layers and compile the model
model %>% 
  layer_dense(units = 32, activation = 'relu', input_shape = c(100)) %>% 
  layer_dense(units = 1, activation = 'sigmoid') %>% 
  compile(
    optimizer = 'rmsprop',
    loss = 'binary_crossentropy',
    metrics = c('accuracy')
  )

# Generate dummy data
data <- matrix(runif(1000*100), nrow = 1000, ncol = 100)
labels <- matrix(round(runif(1000, min = 0, max = 1)), nrow = 1000, ncol = 1)

# Train the model, iterating on the data in batches of 32 samples
model %>% fit(data, labels, epochs=10, batch_size=32)

Here’s a single-input model with 10 classes (categorical classification):

# create model
model <- keras_model_sequential()

# define and compile the model
model %>% 
  layer_dense(units = 32, activation = 'relu', input_shape = c(100)) %>% 
  layer_dense(units = 10, activation = 'softmax') %>% 
  compile(
    optimizer = 'rmsprop',
    loss = 'categorical_crossentropy',
    metrics = c('accuracy')
  )

# Generate dummy data
data <- matrix(runif(1000*100), nrow = 1000, ncol = 100)
labels <- matrix(round(runif(1000, min = 0, max = 9)), nrow = 1000, ncol = 1)

# Convert labels to categorical one-hot encoding
one_hot_labels <- to_categorical(labels, num_classes = 10)

# Train the model, iterating on the data in batches of 32 samples
model %>% fit(data, one_hot_labels, epochs=10, batch_size=32)

Examples

Here are a few examples to get you started!

On the examples page you will also find example models for real datasets:

Some additional examples are provided below.

Multilayer Perceptron (MLP) for multi-class softmax classification

library(keras)

# generate dummy data
x_train <- matrix(runif(1000*20), nrow = 1000, ncol = 20)

y_train <- runif(1000, min = 0, max = 9) %>% 
  round() %>%
  matrix(nrow = 1000, ncol = 1) %>% 
  to_categorical(num_classes = 10)

x_test  <- matrix(runif(100*20), nrow = 100, ncol = 20)

y_test <- runif(100, min = 0, max = 9) %>% 
  round() %>%
  matrix(nrow = 100, ncol = 1) %>% 
  to_categorical(num_classes = 10)

# create model
model <- keras_model_sequential()

# define and compile the model
model %>% 
  layer_dense(units = 64, activation = 'relu', input_shape = c(20)) %>% 
  layer_dropout(rate = 0.5) %>% 
  layer_dense(units = 64, activation = 'relu') %>% 
  layer_dropout(rate = 0.5) %>% 
  layer_dense(units = 10, activation = 'softmax') %>% 
  compile(
    loss = 'categorical_crossentropy',
    optimizer = optimizer_sgd(lr = 0.01, decay = 1e-6, momentum = 0.9, nesterov = TRUE),
    metrics = c('accuracy')     
  )

# train
model %>% fit(x_train, y_train, epochs = 20, batch_size = 128)

# evaluate
score <- model %>% evaluate(x_test, y_test, batch_size = 128)

MLP for binary classification

library(keras)

# generate dummy data
x_train <- matrix(runif(1000*20), nrow = 1000, ncol = 20)
y_train <- matrix(round(runif(1000, min = 0, max = 1)), nrow = 1000, ncol = 1)
x_test <- matrix(runif(100*20), nrow = 100, ncol = 20)
y_test <- matrix(round(runif(100, min = 0, max = 1)), nrow = 100, ncol = 1)

# create model
model <- keras_model_sequential()

# define and compile the model
model %>% 
  layer_dense(units = 64, activation = 'relu', input_shape = c(20)) %>% 
  layer_dropout(rate = 0.5) %>% 
  layer_dense(units = 64, activation = 'relu') %>% 
  layer_dropout(rate = 0.5) %>% 
  layer_dense(units = 1, activation = 'sigmoid') %>% 
  compile(
    loss = 'binary_crossentropy',
    optimizer = 'rmsprop',
    metrics = c('accuracy')
  )

# train 
model %>% fit(x_train, y_train, epochs = 20, batch_size = 128)

# evaluate
score = model %>% evaluate(x_test, y_test, batch_size=128)

VGG-like convnet

library(keras)

# generate dummy data
x_train <- array(runif(100 * 100 * 100 * 3), dim = c(100, 100, 100, 3))

y_train <- runif(100, min = 0, max = 9) %>% 
  round() %>%
  matrix(nrow = 100, ncol = 1) %>% 
  to_categorical(num_classes = 10)

x_test <- array(runif(20 * 100 * 100 * 3), dim = c(20, 100, 100, 3))

y_test <- runif(20, min = 0, max = 9) %>% 
  round() %>%
  matrix(nrow = 20, ncol = 1) %>% 
  to_categorical(num_classes = 10)

# create model
model <- keras_model_sequential()

# define and compile model
# input: 100x100 images with 3 channels -> (100, 100, 3) tensors.
# this applies 32 convolution filters of size 3x3 each.
model %>% 
  layer_conv_2d(filters = 32, kernel_size = c(3,3), activation = 'relu', 
                input_shape = c(100,100,3)) %>% 
  layer_conv_2d(filters = 32, kernel_size = c(3,3), activation = 'relu') %>% 
  layer_max_pooling_2d(pool_size = c(2,2)) %>% 
  layer_dropout(rate = 0.25) %>% 
  layer_conv_2d(filters = 64, kernel_size = c(3,3), activation = 'relu') %>% 
  layer_conv_2d(filters = 64, kernel_size = c(3,3), activation = 'relu') %>% 
  layer_max_pooling_2d(pool_size = c(2,2)) %>% 
  layer_dropout(rate = 0.25) %>% 
  layer_flatten() %>% 
  layer_dense(units = 256, activation = 'relu') %>% 
  layer_dropout(rate = 0.25) %>% 
  layer_dense(units = 10, activation = 'softmax') %>% 
  compile(
    loss = 'categorical_crossentropy', 
    optimizer = optimizer_sgd(lr = 0.01, decay = 1e-6, momentum = 0.9, nesterov = TRUE)
  )
  
# train
model %>% fit(x_train, y_train, batch_size = 32, epochs = 10)

# evaluate
score <- model %>% evaluate(x_test, y_test, batch_size = 32)

Sequence classification with LSTM

model <- keras_model_sequential() 
model %>% 
  layer_embedding(input_dim = max_features, output_dim - 256) %>% 
  layer_lstm(units = 128) %>% 
  layer_dropout(rate = 0.5) %>% 
  layer_dense(units = 1, activation = 'sigmoid') %>% 
  compile(
    loss = 'binary_crossentropy',
    optimizer = 'rmsprop',
    metrics = c('accuracy')
  )

model %>% fit(x_train, y_train, batch_size = 16, epochs = 10)
score <- model %>% evaluate(x_test, y_test, batch_size = 16)

Sequence classification with 1D convolutions:

model <- keras_model_sequential()
model %>% 
  layer_conv_1d(filters = 64, kernel_size = 3, activation = 'relu',
                input_shape = c(seq_length, 100)) %>% 
  layer_conv_1d(filters = 64, kernel_size = 3, activation = 'relu') %>% 
  layer_max_pooling_1d(pool_size = 3) %>% 
  layer_conv_1d(filters = 128, kernel_size = 3, activation = 'relu') %>% 
  layer_conv_1d(filters = 128, kernel_size = 3, activation = 'relu') %>% 
  layer_global_average_pooling_1d() %>% 
  layer_dropout(rate = 0.5) %>% 
  layer_dense(units = 1, activation = 'sigmoid') %>% 
  compile(
    loss = 'binary_crossentropy',
    optimizer = 'rmsprop',
    metrics = c('accuracy')
  )

model %>% fit(x_train, y_train, batch_size = 16, epochs = 10)
score <- model %>% evaluate(x_test, y_test, batch_size = 16)

Stacked LSTM for sequence classification

In this model, we stack 3 LSTM layers on top of each other, making the model capable of learning higher-level temporal representations.

The first two LSTMs return their full output sequences, but the last one only returns the last step in its output sequence, thus dropping the temporal dimension (i.e. converting the input sequence into a single vector).

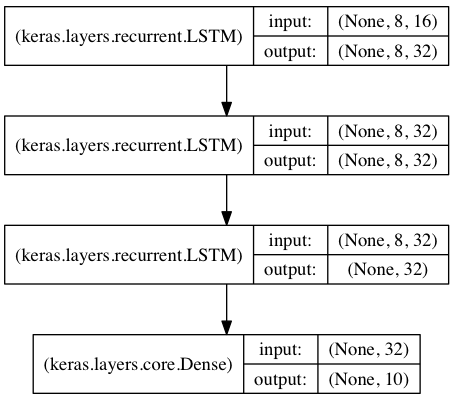
stacked LSTM

library(keras)

# constants
data_dim <- 16
timesteps <- 8
num_classes <- 10

# define and compile model
# expected input data shape: (batch_size, timesteps, data_dim)
model <- keras_model_sequential() 
model %>% 
  layer_lstm(units = 32, return_sequences = TRUE, input_shape = c(timesteps, data_dim)) %>% 
  layer_lstm(units = 32, return_sequences = TRUE) %>% 
  layer_lstm(units = 32) %>% # return a single vector dimension 32
  layer_dense(units = 10, activation = 'softmax') %>% 
  compile(
    loss = 'categorical_crossentropy',
    optimizer = 'rmsprop',
    metrics = c('accuracy')
  )
  
# generate dummy training data
x_train <- array(runif(1000 * timesteps * data_dim), dim = c(1000, timesteps, data_dim))
y_train <- matrix(runif(1000 * num_classes), nrow = 1000, ncol = num_classes)

# generate dummy validation data
x_val <- array(runif(100 * timesteps * data_dim), dim = c(100, timesteps, data_dim))
y_val <- matrix(runif(100 * num_classes), nrow = 100, ncol = num_classes)

# train
model %>% fit( 
  x_train, y_train, batch_size = 64, epochs = 5, validation_data = list(x_val, y_val)
)

Same stacked LSTM model, rendered “stateful”

A stateful recurrent model is one for which the internal states (memories) obtained after processing a batch of samples are reused as initial states for the samples of the next batch. This allows to process longer sequences while keeping computational complexity manageable.

library(keras)

# constants
data_dim <- 16
timesteps <- 8
num_classes <- 10
batch_size <- 32

# define and compile model
# Expected input batch shape: (batch_size, timesteps, data_dim)
# Note that we have to provide the full batch_input_shape since the network is stateful.
# the sample of index i in batch k is the follow-up for the sample i in batch k-1.
model <- keras_model_sequential()
model %>% 
  layer_lstm(units = 32, return_sequences = TRUE, stateful = TRUE,
             batch_input_shape = c(batch_size, timesteps, data_dim)) %>% 
  layer_lstm(units = 32, return_sequences = TRUE, stateful = TRUE) %>% 
  layer_lstm(units = 32, stateful = TRUE) %>% 
  layer_dense(units = 10, activation = 'softmax') %>% 
  compile(
    loss = 'categorical_crossentropy',
    optimizer = 'rmsprop',
    metrics = c('accuracy')
  )
  
# generate dummy training data
x_train <- array(runif( (batch_size * 10) * timesteps * data_dim), 
                 dim = c(batch_size * 10, timesteps, data_dim))
y_train <- matrix(runif( (batch_size * 10) * num_classes), 
                  nrow = batch_size * 10, ncol = num_classes)

# generate dummy validation data
x_val <- array(runif( (batch_size * 3) * timesteps * data_dim), 
               dim = c(batch_size * 3, timesteps, data_dim))
y_val <- matrix(runif( (batch_size * 3) * num_classes), 
                nrow = batch_size * 3, ncol = num_classes)

# train
model %>% fit( 
  x_train, 
  y_train, 
  batch_size = batch_size, 
  epochs = 5, 
  shuffle = FALSE,
  validation_data = list(x_val, y_val)
)